The library contains a single comprehensive regression test.
For a given container type in this library, the test creates
an object of the container type and an object of the
corresponding standard type (e.g., std::set). It
then performs a random sequence of methods with random
arguments (e.g., inserts, erases, and so forth) on both
objects. At each operation, the test checks the return value of
the method, and optionally both compares this library's
object with the standard's object as well as performing other
consistency checks on this library's object (e.g.,
order preservation, when applicable, or node invariants, when
applicable).
Additionally, the test integrally checks exception safety and resource leaks. This is done as follows. A special allocator type, written for the purpose of the test, both randomly throws an exceptions when allocations are performed, and tracks allocations and de-allocations. The exceptions thrown at allocations simulate memory-allocation failures; the tracking mechanism checks for memory-related bugs (e.g., resource leaks and multiple de-allocations). Both this library's containers and the containers' value-types are configured to use this allocator.
For granularity, the test is split into the several sources, each checking only some containers.
For more details, consult the files in
testsuite/ext/pb_ds/regression.
This test inserts a number of values with keys from an
arbitrary text ([biblio.wickland96thirty]) into a container,
then performs a series of finds using
find . It measures the average
time for find as a function of
the number of values inserted.
It uses the test file:
performance/ext/pb_ds/text_find_timing_test.cc
And uses the data file:
filethirty_years_among_the_dead_preproc.txt
The test checks the effect of different range-hashing functions, trigger policies, and cache-hashing policies.
The graphic below show the results for the native
and collision-chaining hash types the function
applied being a text find timing test using
find.
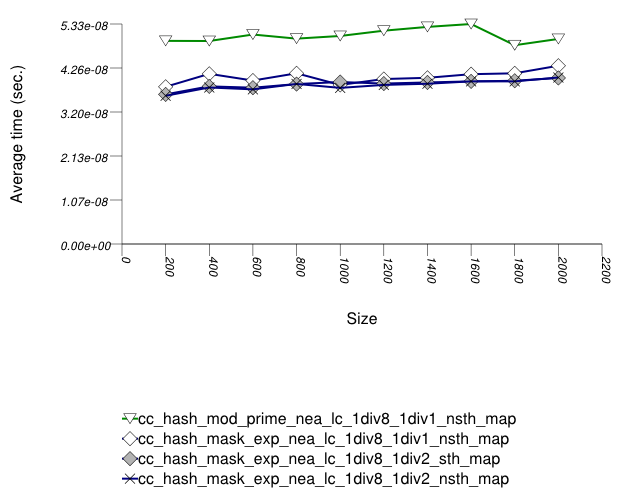
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_sth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| cc_hash_mask_exp_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
In this setting, the range-hashing scheme affects performance more than other policies. As the results show, containers using mod-based range-hashing (including the native hash-based container, which is currently hard-wired to this scheme) have lower performance than those using mask-based range-hashing. A modulo-based range-hashing scheme's main benefit is that it takes into account all hash-value bits. Standard string hash-functions are designed to create hash values that are nearly-uniform as is ([biblio.knuth98sorting]).
Trigger policies, i.e. the load-checks constants, affect performance to a lesser extent.
Perhaps surprisingly, storing the hash value alongside each
entry affects performance only marginally, at least in this
library's implementation. (Unfortunately, it was not possible to run
the tests with std::tr1::unordered_map 's
cache_hash_code = true , as it appeared to
malfuntion.)
This test inserts a number of values with uniform
integer keys into a container, then performs a series of finds
using find. It measures the average time
for find as a function of the number of values
inserted.
It uses the test file:
performance/ext/pb_ds/random_int_find_timing.cc
The test checks the effect of different underlying hash-tables, range-hashing functions, and trigger policies.
There are two sets of results for this type, one for collision-chaining hashes, and one for general-probe hashes.
The first graphic below shows the results for the native and
collision-chaining hash types. The function applied being a random
integer timing test using find.
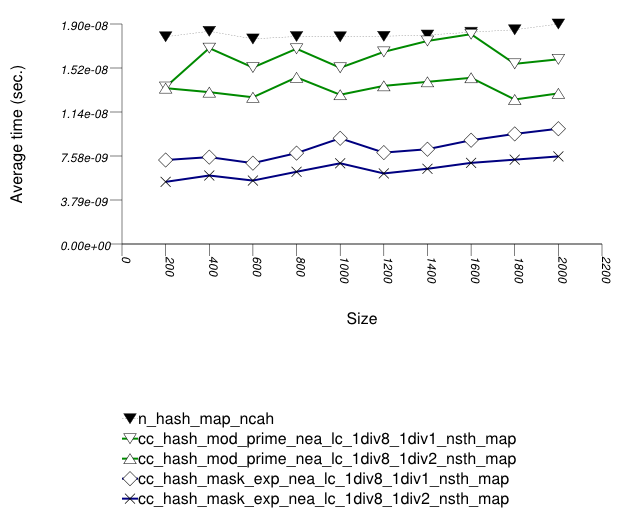
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mod_prime_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| cc_hash_mask_exp_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
And the second graphic shows the results for the native and
general-probe hash types. The function applied being a random
integer timing test using find.
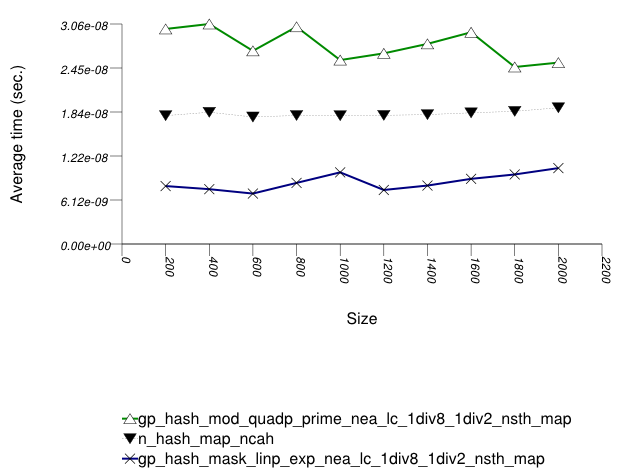
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| gp_hash_mod_quadp_prime_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Probe_Fn
|
quadratic_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| gp_hash_mask_linp_exp_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Probe_Fn
|
linear_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
In this setting, the choice of underlying hash-table affects performance most, then the range-hashing scheme and, only finally, other policies.
When comparing probing and chaining containers, it is
apparent that the probing containers are less efficient than the
collision-chaining containers (
std::tr1::unordered_map uses
collision-chaining) in this case.
Hash-Based Integer Subscript Insert Timing Test shows a different case, where the situation is reversed;
Within each type of hash-table, the range-hashing scheme
affects performance more than other policies; Hash-Based Text
find Find Timing Test also shows this. In the
above graphics should be noted that
std::tr1::unordered_map are hard-wired
currently to mod-based schemes.
This test inserts a number of values with uniform
integer keys into a container, then performs a series of finds
using operator[]. It measures the average time
for operator[] as a function of the number of
values inserted.
It uses the test file:
performance/ext/pb_ds/random_int_subscript_find_timing.cc
The test checks the effect of different underlying hash-tables, range-hashing functions, and trigger policies.
There are two sets of results for this type, one for collision-chaining hashes, and one for general-probe hashes.
The first graphic below shows the results for the native
and collision-chaining hash types, using as the function
applied an integer subscript timing test with
find.
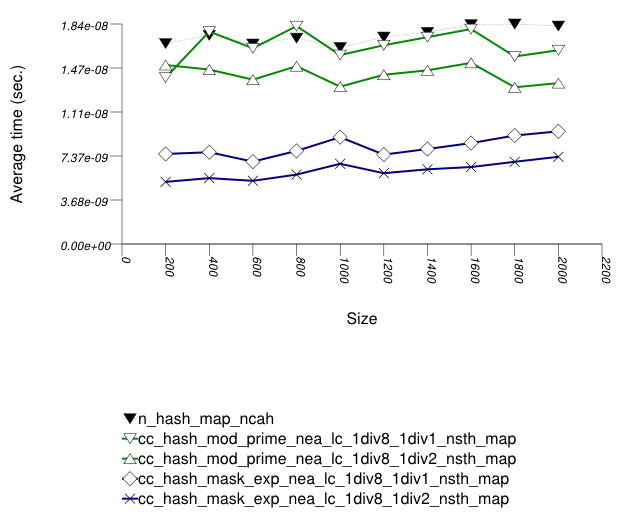
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mod_prime_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| cc_hash_mask_exp_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
And the second graphic shows the results for the native and
general-probe hash types. The function applied being a random
integer timing test using find.
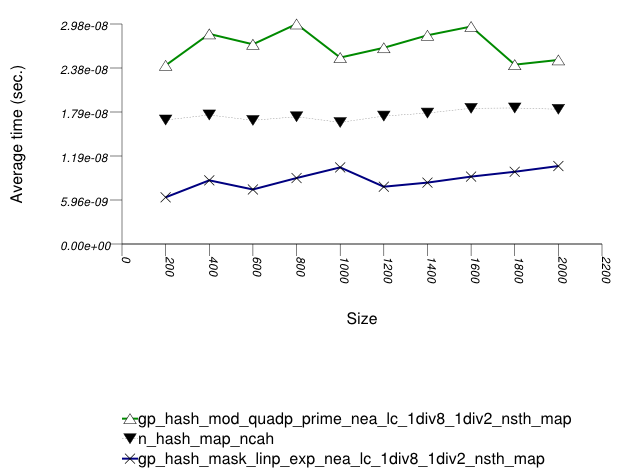
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| gp_hash_mod_quadp_prime_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Probe_Fn
|
quadratic_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| gp_hash_mask_linp_exp_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Probe_Fn
|
linear_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
This test inserts a number of values with uniform i.i.d.
integer keys into a container, using
operator[]. It measures the average time for
operator[] as a function of the number of
values inserted.
It uses the test file:
performance/ext/pb_ds/random_int_subscript_insert_timing.cc
The test checks the effect of different underlying hash-tables.
There are two sets of results for this type, one for collision-chaining hashes, and one for general-probe hashes.
The first graphic below shows the results for the native
and collision-chaining hash types, using as the function
applied an integer subscript timing test with
insert.
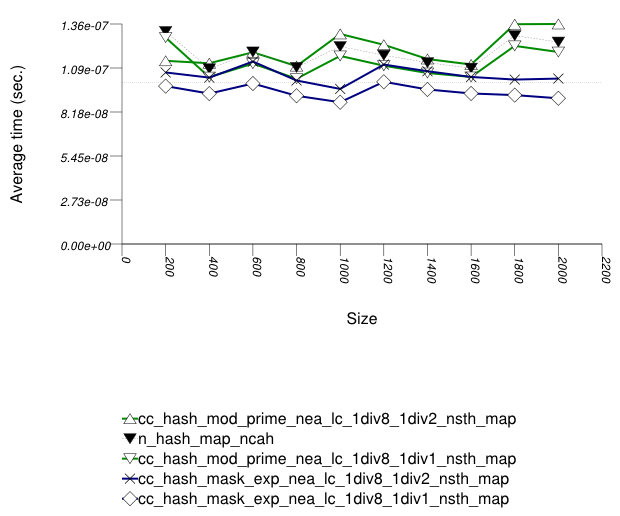
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mod_prime_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| cc_hash_mask_exp_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
And the second graphic shows the results for the native and
general-probe hash types. The function applied being a random
integer timing test using find.
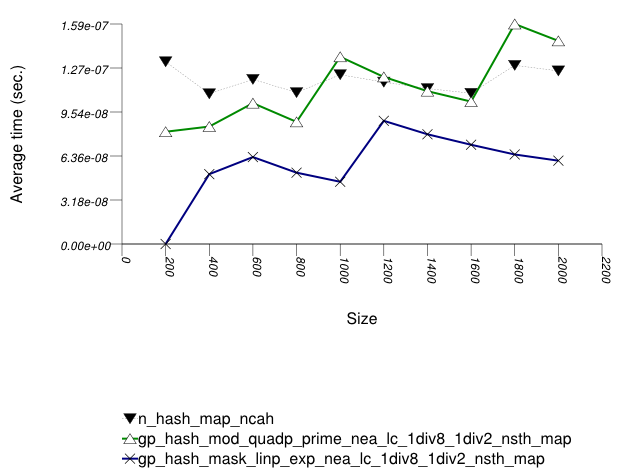
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| gp_hash_mod_quadp_prime_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Probe_Fn
|
quadratic_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| gp_hash_mask_linp_exp_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Probe_Fn
|
linear_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
In this setting, as in Hash-Based Text
find Find Timing test and Hash-Based
Integer find Find Timing test , the choice
of underlying hash-table underlying hash-table affects performance
most, then the range-hashing scheme, and
finally any other policies.
There are some differences, however:
In this setting, probing tables function sometimes more efficiently than collision-chaining tables. This is explained shortly.
The performance graphs have a "saw-tooth" shape. The average insert time rises and falls. As values are inserted into the container, the load factor grows larger. Eventually, a resize occurs. The reallocations and rehashing are relatively expensive. After this, the load factor is smaller than before.
Collision-chaining containers use indirection for greater flexibility; probing containers store values contiguously, in an array (see Figure Motivation::Different underlying data structures A and B, respectively). It follows that for simple data types, probing containers access their allocator less frequently than collision-chaining containers, (although they still have less efficient probing sequences). This explains why some probing containers fare better than collision-chaining containers in this case.
Within each type of hash-table, the range-hashing scheme affects
performance more than other policies. This is similar to the
situation in Hash-Based Text
find Find Timing Test and Hash-Based
Integer find Find Timing Test.
Unsurprisingly, however, containers with lower αmax perform worse in this case,
since more re-hashes are performed.
This test inserts a number of values with a markedly
non-uniform integer keys into a container, then performs
a series of finds using find. It measures the average
time for find as a function of the number of values in
the containers. The keys are generated as follows. First, a
uniform integer is created. Then it is then shifted left 8 bits.
It uses the test file:
performance/ext/pb_ds/hash_zlob_random_int_find_timing.cc
The test checks the effect of different range-hashing functions and trigger policies.
The graphic below show the results for the native, collision-chaining, and general-probing hash types.
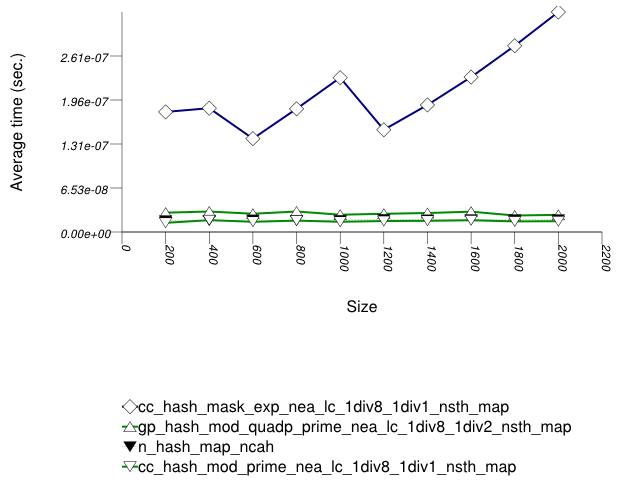
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| gp_hash_mod_quadp_prime_1div2_nsth_map | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Probe_Fn
|
quadratic_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
In this setting, the distribution of keys is so skewed that
the underlying hash-table type affects performance marginally.
(This is in contrast with Hash-Based Text
find Find Timing Test, Hash-Based
Integer find Find Timing Test, Hash-Based
Integer Subscript Find Timing Test and Hash-Based
Integer Subscript Insert Timing Test.)
The range-hashing scheme affects performance dramatically. A
mask-based range-hashing scheme effectively maps all values
into the same bucket. Access degenerates into a search within
an unordered linked-list. In the graphic above, it should be noted that
std::tr1::unordered_map is hard-wired currently to mod-based and mask-based schemes,
respectively.
When observing the settings of this test, it is apparent
that the keys' distribution is far from natural. One might ask
if the test is not contrived to show that, in some cases,
mod-based range hashing does better than mask-based range
hashing. This is, in fact just the case. A
more natural case in which mod-based range hashing is better was not encountered.
Thus the inescapable conclusion: real-life key distributions are handled better
with an appropriate hash function and a mask-based
range-hashing function. (pb_ds/example/hash_shift_mask.cc
shows an example of handling this a-priori known skewed
distribution with a mask-based range-hashing function). If hash
performance is bad, a χ2 test can be used
to check how to transform it into a more uniform
distribution.
For this reason, this library's default range-hashing function is mask-based.
This test inserts a number of uniform integer keys into a container, then erases all keys except one. It measures the final size of the container.
It uses the test file:
performance/ext/pb_ds/hash_random_int_erase_mem_usage.cc
The test checks how containers adjust internally as their logical size decreases.
The graphic below show the results for the native, collision-chaining, and general-probing hash types.
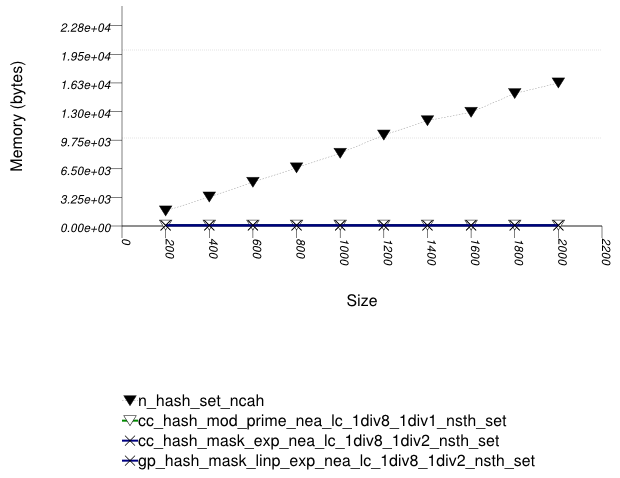
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details |
|---|---|---|---|---|
| n_hash_map_ncah | ||||
std::tr1::unordered_map
|
cache_hash_code
|
false
| ||
| cc_hash_mod_prime_1div1_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mod_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_prime_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/1
| |||
| cc_hash_mask_exp_1div2_nsth_map | ||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
| gp_hash_mask_linp_exp_1div2_nsth_set | ||||
gp_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||
Probe_Fn
|
linear_probe_fn
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||
The standard's hash-based containers act very differently than trees in this respect. When erasing numerous keys from an standard associative-container, the resulting memory user varies greatly depending on whether the container is tree-based or hash-based. This is a fundamental consequence of the standard's interface for associative containers, and it is not due to a specific implementation.
This test inserts a number of values with keys from an arbitrary
text ([ wickland96thirty ]) into a container
using insert . It measures the average time
for insert as a function of the number of
values inserted.
The test checks the effect of different underlying data structures.
It uses the test file:
performance/ext/pb_ds/tree_text_insert_timing.cc
The three graphics below show the results for the native tree and this library's node-based trees, the native tree and this library's vector-based trees, and the native tree and this library's PATRICIA-trie, respectively.
The graphic immediately below shows the results for the native tree type and several node-based tree types.
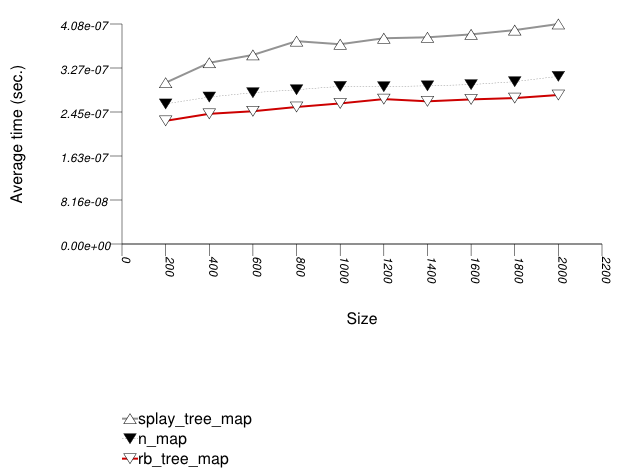
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_map | ||
std::map
| ||
| splay_tree_map | ||
tree
|
Tag
|
splay_tree_tag
|
Node_update
|
null_node_update
| |
| rb_tree_map | ||
tree
|
Tag
|
rb_tree_tag
|
Node_update
|
null_node_update
| |
The graphic below shows the results for the native tree type and a vector-based tree type.
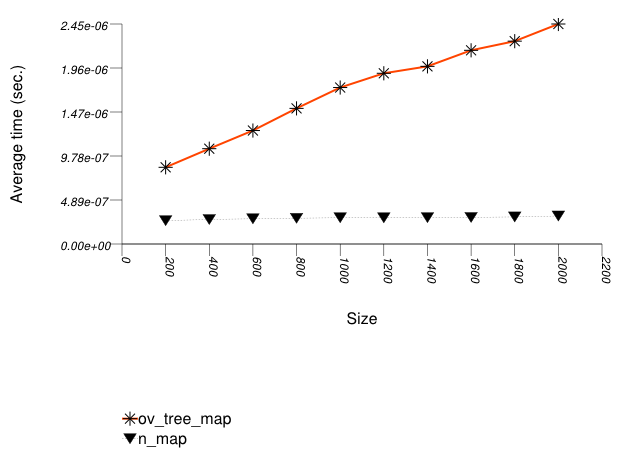
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_map | ||
std::map
| ||
| ov_tree_map | ||
tree
|
Tag
|
ov_tree_tag
|
Node_update
|
null_node_update
| |
The graphic below shows the results for the native tree type and a PATRICIA trie type.
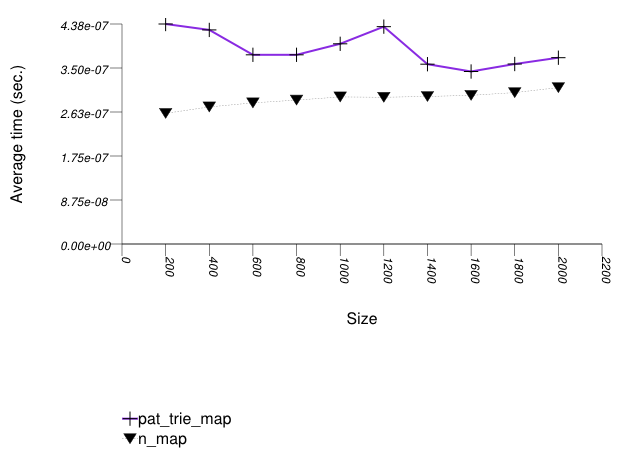
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_map | ||
std::map
| ||
| pat_trie_map | ||
tree
|
Tag
|
pat_trie_tag
|
Node_update
|
null_node_update
| |
Observing the first graphic implies that for this setting, a splay tree
(tree with Tag
= splay_tree_tag) does not do
well. See also the Branch-Based
Text find Find Timing Test. The two
red-black trees perform better.
Observing the second graphic, an ordered-vector tree
(tree with Tag
= ov_tree_tag) performs
abysmally. Inserting into this type of tree has linear complexity
[ austern00noset].
Observing the third and last graphic, A PATRICIA trie
(trie with Tag
= pat_trie_tag) has abysmal
performance, as well. This is not that surprising, since a
large-fan-out PATRICIA trie works like a hash table with
collisions resolved by a sub-trie. Each time a collision is
encountered, a new "hash-table" is built A large fan-out PATRICIA
trie, however, doe does well in look-ups (see Branch-Based
Text find Find Timing Test). It may be
beneficial in semi-static settings.
This test inserts a number of values with keys from an
arbitrary text ([wickland96thirty]) into
a container, then performs a series of finds using
find. It measures the average time
for find as a function of the number of
values inserted.
It uses the test file:
performance/ext/pb_ds/text_find_timing.cc
The test checks the effect of different underlying data structures.
The graphic immediately below shows the results for the native tree type and several other tree types.
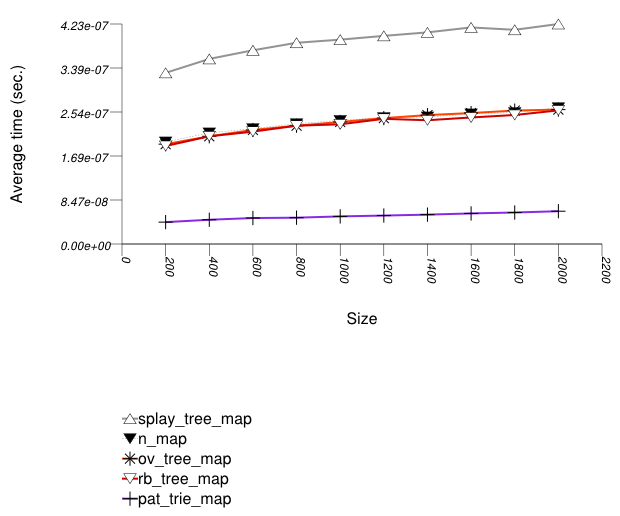
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_map | ||
std::map
| ||
| splay_tree_map | ||
tree
|
Tag
|
splay_tree_tag
|
Node_Update
|
null_node_update
| |
| rb_tree_map | ||
tree
|
Tag
|
rb_tree_tag
|
Node_Update
|
null_node_update
| |
| ov_tree_map | ||
tree
|
Tag
|
ov_tree_tag
|
Node_Update
|
null_node_update
| |
| pat_trie_map | ||
tree
|
Tag
|
pat_trie_tag
|
Node_Update
|
null_node_update
| |
For this setting, a splay tree (tree
with Tag
= splay_tree_tag) does not do
well. This is possibly due to two reasons:
A splay tree is not guaranteed to be balanced [motwani95random]. If a splay tree contains n nodes, its average root-leaf path can be m >> log(n).
Assume a specific root-leaf search path has length m, and the search-target node has distance m' from the root. A red-black tree will require m + 1 comparisons to find the required node; a splay tree will require 2 m' comparisons. A splay tree, consequently, can perform many more comparisons than a red-black tree.
An ordered-vector tree (tree
with Tag = ov_tree_tag), a red-black
tree (tree
with Tag = rb_tree_tag), and the
native red-black tree all share approximately the same
performance.
An ordered-vector tree is slightly slower than red-black trees, since it requires, in order to find a key, more math operations than they do. Conversely, an ordered-vector tree requires far lower space than the others. ([austern00noset], however, seems to have an implementation that is also faster than a red-black tree).
A PATRICIA trie (trie
with Tag = pat_trie_tag) has good
look-up performance, due to its large fan-out in this case. In
this setting, a PATRICIA trie has look-up performance comparable
to a hash table (see Hash-Based Text
find Timing Test), but it is order
preserving. This is not that surprising, since a large-fan-out
PATRICIA trie works like a hash table with collisions resolved
by a sub-trie. A large-fan-out PATRICIA trie does not do well on
modifications (see Tree-Based and Trie-Based
Text Insert Timing Test). Therefore, it is possibly beneficial in
semi-static settings.
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
a container, then performs a series of finds using
find. It is different than Tree-Based and
Trie-Based Text find Find Timing Test in the
sequence of finds it performs: this test performs multiple
finds on the same key before moving on to the next
key. It measures the average time for find as a
function of the number of values inserted.
It uses the test file:
performance/ext/pb_ds/tree_text_lor_find_timing.cc
The test checks the effect of different underlying data structures in a locality-of-reference setting.
The graphic immediately below shows the results for the native tree type and several other tree types.
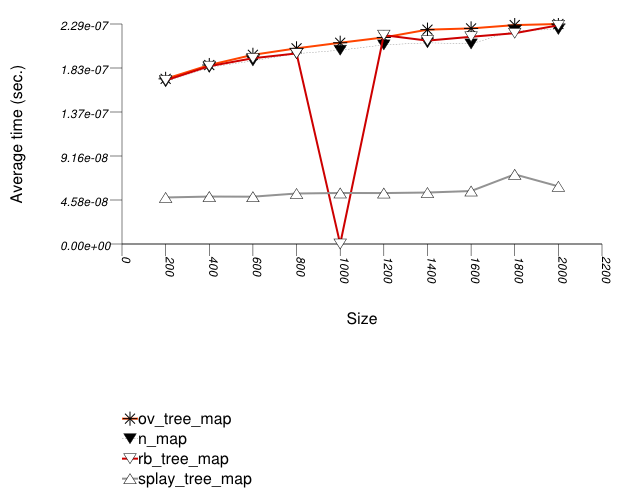
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_map | ||
std::map
| ||
| splay_tree_map | ||
tree
|
Tag
|
splay_tree_tag
|
Node_Update
|
null_node_update
| |
| rb_tree_map | ||
tree
|
Tag
|
rb_tree_tag
|
Node_Update
|
null_node_update
| |
| ov_tree_map | ||
tree
|
Tag
|
ov_tree_tag
|
Node_Update
|
null_node_update
| |
| pat_trie_map | ||
tree
|
Tag
|
pat_trie_tag
|
Node_Update
|
null_node_update
| |
For this setting, an ordered-vector tree
(tree with Tag
= ov_tree_tag), a red-black tree
(tree with Tag
= rb_tree_tag), and the native red-black
tree all share approximately the same performance.
A splay tree (tree
with Tag = splay_tree_tag) does
much better, since each (successful) find "bubbles" the
corresponding node to the root of the tree.
This test a container, inserts into a number of values, splits
the container at the median, and joins the two containers. (If the
containers are one of this library's trees,
it splits and joins with the split and
join method; otherwise, it uses the erase and
insert methods.) It measures the time for splitting
and joining the containers as a function of the number of
values inserted.
It uses the test file:
performance/ext/pb_ds/tree_split_join_timing.cc
The test checks the performance difference of join
as opposed to a sequence of insert operations; by
implication, this test checks the most efficient way to erase a
sub-sequence from a tree-like-based container, since this can
always be performed by a small sequence of splits and joins.
The graphic immediately below shows the results for the native tree type and several other tree types.
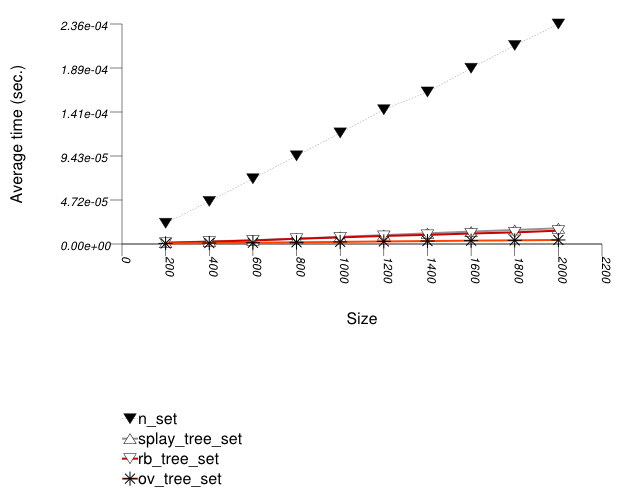
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_set | ||
std::set
| ||
| splay_tree_set | ||
tree
|
Tag
|
splay_tree_tag
|
Node_Update
|
null_node_update
| |
| rb_tree_set | ||
tree
|
Tag
|
rb_tree_tag
|
Node_Update
|
null_node_update
| |
| ov_tree_set | ||
tree
|
Tag
|
ov_tree_tag
|
Node_Update
|
null_node_update
| |
| pat_trie_map | ||
tree
|
Tag
|
pat_trie_tag
|
Node_Update
|
null_node_update
| |
In this test, the native red-black trees must be split and
joined externally, through a sequence of erase and
insert operations. This is clearly
super-linear, and it is not that surprising that the cost is
high.
This library's tree-based containers use in this test the
split and join methods,
which have lower complexity: the join method
of a splay tree (tree
with Tag
= splay_tree_tag) is quadratic in the
length of the longest root-leaf path, and linear in the total
number of elements; the join method of a
red-black tree (tree
with Tag
= rb_tree_tag) or an ordered-vector tree
(tree with Tag
= ov_tree_tag) is linear in the number of
elements.
Asides from orders of growth, this library's trees access their
allocator very little in these operations, and some of them do not
access it at all. This leads to lower constants in their
complexity, and, for some containers, to exception-free splits and
joins (which can be determined
via container_traits).
It is important to note that split and
join are not esoteric methods - they are the most
efficient means of erasing a contiguous range of values from a
tree based container.
This test creates a container, inserts random integers into the
the container, and then checks the order-statistics of the
container's values. (If the container is one of this
library's trees, it does this with
the order_of_key method of
tree_order_statistics_node_update
; otherwise, it uses the find method and
std::distance.) It measures the average
time for such queries as a function of the number of values
inserted.
It uses the test file:
performance/ext/pb_ds/tree_order_statistics_timing.cc
The test checks the performance difference of policies based on node-invariant as opposed to a external functions.
The graphic immediately below shows the results for the native tree type and several other tree types.
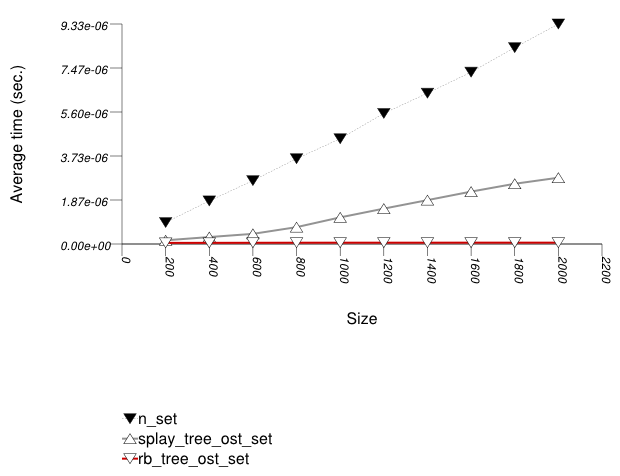
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_set | ||
std::set
| ||
| splay_tree_ost_set | ||
tree
|
Tag
|
splay_tree_tag
|
Node_Update
|
tree_order_statistics_node_update
| |
| rb_tree_ost_set | ||
tree
|
Tag
|
rb_tree_tag
|
Node_Update
|
tree_order_statistics_node_update
| |
In this test, the native red-black tree can support
order-statistics queries only externally, by performing a
find (alternatively, lower_bound or
upper_bound ) and then using std::distance .
This is clearly linear, and it is not that surprising that the
cost is high.
This library's tree-based containers use in this test the
order_of_key method of tree_order_statistics_node_update.
This method has only linear complexity in the length of the
root-node path. Unfortunately, the average path of a splay tree
(tree
with Tag = splay_tree_tag ) can
be higher than logarithmic; the longest path of a red-black
tree (tree
with Tag = rb_tree_tag ) is
logarithmic in the number of elements. Consequently, the splay
tree has worse performance than the red-black tree.
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform i.i.d.integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key (see Motivation::Associative Containers::Alternative to Multiple Equivalent Keys). There are 400 distinct primary keys, and the ratio of secondary keys to primary keys ranges from 1 to 5.
The test measures the average find-time as a function of the
number of values inserted. For this library's containers, it
finds the secondary key from a container obtained from finding
a primary key. For the native multimaps, it searches a range
obtained using std::equal_range on a primary key.
It uses the test file:
performance/ext/pb_ds/multimap_text_find_timing_small.cc
The test checks the find-time scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.
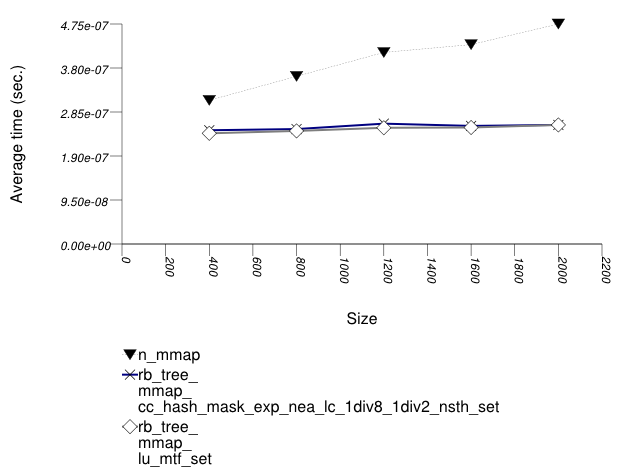
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.
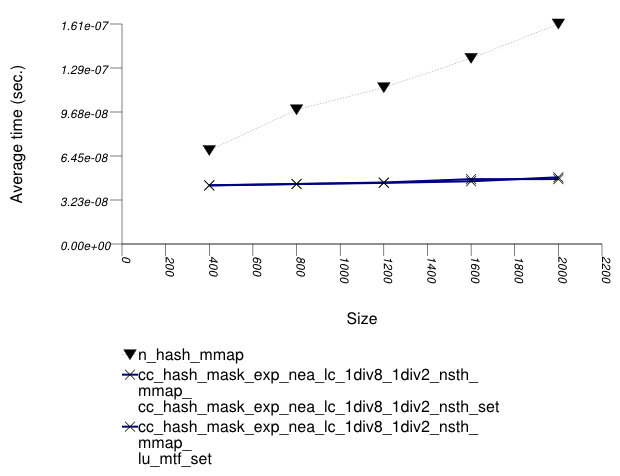
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key. There are 400 distinct primary keys, and the ratio of secondary keys to primary keys ranges from 1 to 5.
The test measures the average find-time as a function of the
number of values inserted. For this library's containers, it
finds the secondary key from a container obtained from finding
a primary key. For the native multimaps, it searches a range
obtained using std::equal_range on a primary key.
It uses the test file:
performance/ext/pb_ds/multimap_text_find_timing_large.cc
The test checks the find-time scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.
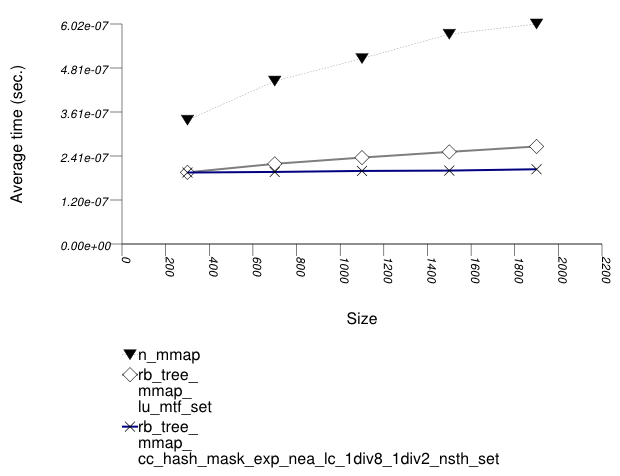
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.
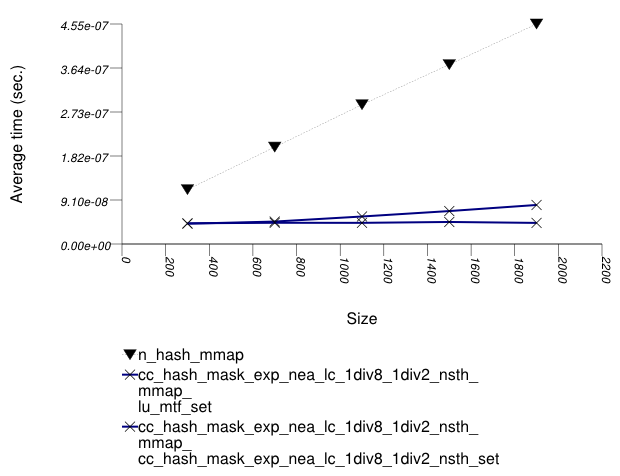
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key. There are 400 distinct primary keys, and the ratio of secondary keys to primary keys ranges from 1 to 5.
The test measures the average insert-time as a function of
the number of values inserted. For this library's containers,
it inserts a primary key into the primary associative
container, then a secondary key into the secondary associative
container. For the native multimaps, it obtains a range using
std::equal_range, and inserts a value only if it was
not contained already.
It uses the test file:
performance/ext/pb_ds/multimap_text_insert_timing_small.cc
The test checks the insert-time scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.
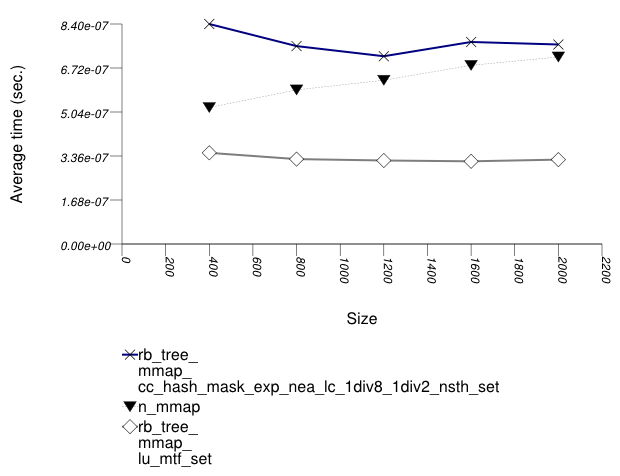
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key. There are 400 distinct primary keys, and the ratio of secondary keys to primary keys ranges from 1 to 5.
The test measures the average insert-time as a function of
the number of values inserted. For this library's containers,
it inserts a primary key into the primary associative
container, then a secondary key into the secondary associative
container. For the native multimaps, it obtains a range using
std::equal_range, and inserts a value only if it was
not contained already.
It uses the test file:
performance/ext/pb_ds/multimap_text_insert_timing_large.cc
The test checks the insert-time scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.
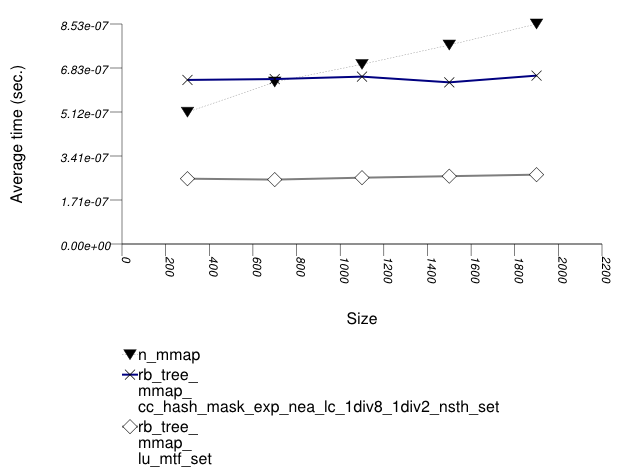
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key. There are 100 distinct primary keys, and the ratio of secondary keys to primary keys ranges to about 20.
The test measures the memory use as a function of the number of values inserted.
It uses the test file:
performance/ext/pb_ds/multimap_text_insert_mem_usage_small.cc
The test checks the memory scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of pairs into a container. The first item of each pair is a string from an arbitrary text [wickland96thirty], and the second is a uniform integer. The container is a "multimap" - it considers the first member of each pair as a primary key, and the second member of each pair as a secondary key. There are 100 distinct primary keys, and the ratio of secondary keys to primary keys ranges to about 20.
The test measures the memory use as a function of the number of values inserted.
It uses the test file:
performance/ext/pb_ds/multimap_text_insert_mem_usage_large.cc
The test checks the memory scalability of different "multimap" designs.
The graphic below show the results for "multimaps" which use a tree-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_mmap | ||||||
std::multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
tree
|
Tag
|
rb_tree_tag
| ||||
Node_Update
|
null_node_update
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
The graphic below show the results for "multimaps" which use a hash-based container for primary keys.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details | Parameter | Details | Parameter | Details |
|---|---|---|---|---|---|---|
| n_hash_mmap | ||||||
std::tr1::unordered_multimap
| ||||||
| rb_tree_mmap_lu_mtf_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
list_update
|
Update_Policy
|
lu_move_to_front_policy
| |||
| rb_tree_mmap_cc_hash_mask_exp_1div2_nsth_set | ||||||
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| ||||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
Mapped
|
cc_hash_table
|
Comb_Hash_Fn
|
direct_mask_range_hashing
| |||
Resize_Policy
|
hash_standard_resize_policy
|
Size_Policy
|
hash_exponential_size_policy
| |||
Trigger_Policy
|
hash_load_check_resize_trigger with
αmin = 1/8 and αmax = 1/2
| |||||
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
a container using push. It measures the average time
for push as a function of the number of values
pushed.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_push_timing.cc
The test checks the effect of different underlying data structures.
The two graphics below show the results for the native priority_queues and this library's priority_queues.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
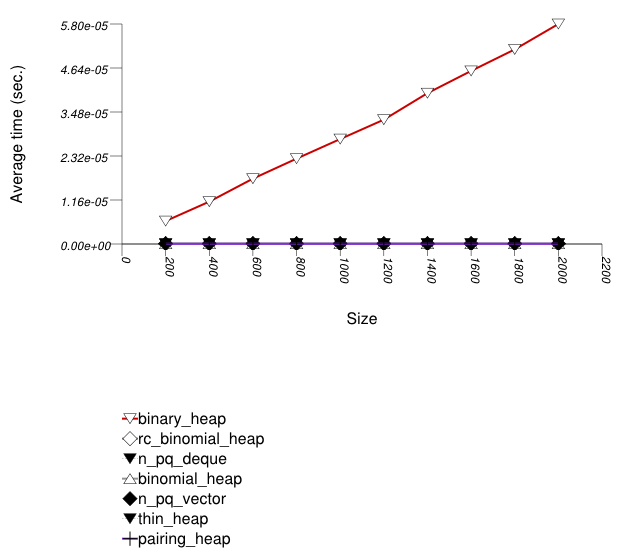
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The graphic below shows the results for the binary-heap based native priority queues and this library's pairing-heap priority_queue data structures.
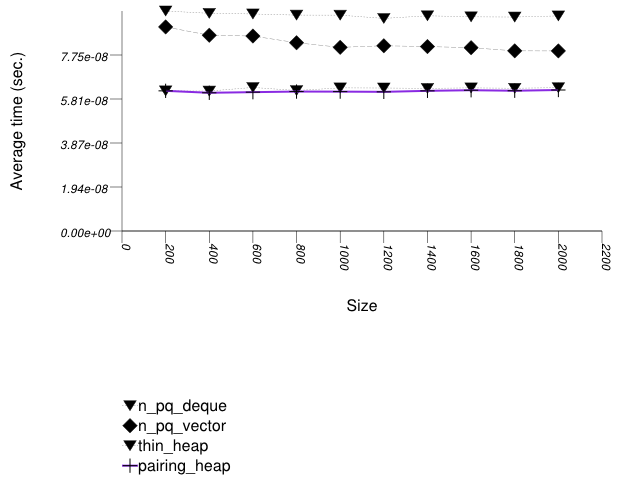
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
Pairing heaps (priority_queue with
Tag = pairing_heap_tag)
are the most suited for sequences of push and
pop operations of non-primitive types (e.g.
std::strings). (See Priority Queue
Text push and pop Timing Test.) They are
less constrained than binomial heaps, e.g., and since
they are node-based, they outperform binary heaps. (See
Priority
Queue Random Integer push Timing Test for the case
of primitive types.)
The standard's priority queues do not seem to perform well in
this case: the std::vector implementation needs to
perform a logarithmic sequence of string operations for each
operation, and the deque implementation is possibly hampered by
its need to manipulate a relatively-complex type (deques
support a O(1) push_front, even though it is
not used by std::priority_queue.)
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
a container using push , then removes them using
pop . It measures the average time for push
as a function of the number of values.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_push_pop_timing.cc
The test checks the effect of different underlying data structures.
The two graphics below show the results for the native priority_queues and this library's priority_queues.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
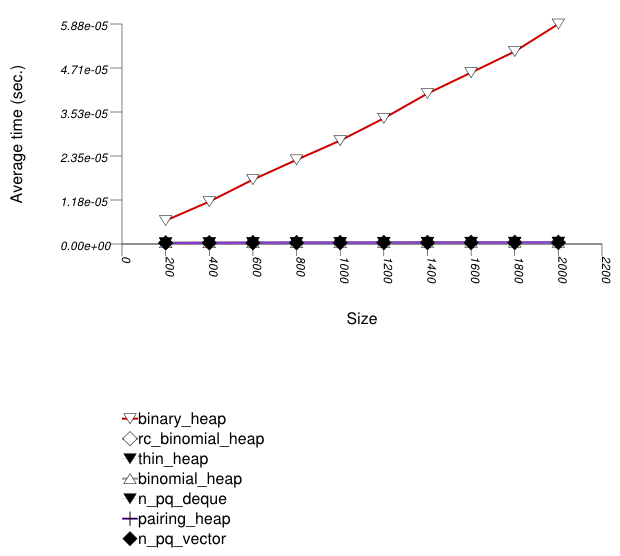
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The graphic below shows the results for the native priority queues and this library's pairing-heap priority_queue data structures.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue adapting std::vector
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
These results are very similar to Priority Queue Text
push Timing Test. As stated there, pairing heaps
(priority_queue with
Tag
= pairing_heap_tag) are most suited
for push and pop
sequences of non-primitive types such as strings. Observing these
two tests, one can note that a pairing heap outperforms the others
in terms of push operations, but equals
binary heaps (priority_queue with
Tag
= binary_heap_tag) if the number
of push and pop
operations is equal. As the number of pop
operations is at most equal to the number
of push operations, pairing heaps are better
in this case. See Priority Queue Random
Integer push and pop
Timing Test for a case which is different.
This test inserts a number of values with integer keys
into a container using push. It
measures the average time for push as a
function of the number of values.
It uses the test file:
performance/ext/pb_ds/priority_queue_random_int_push_timing.cc
The test checks the effect of different underlying data structures.
The two graphics below show the results for the native priority_queues and this library's priority_queues.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
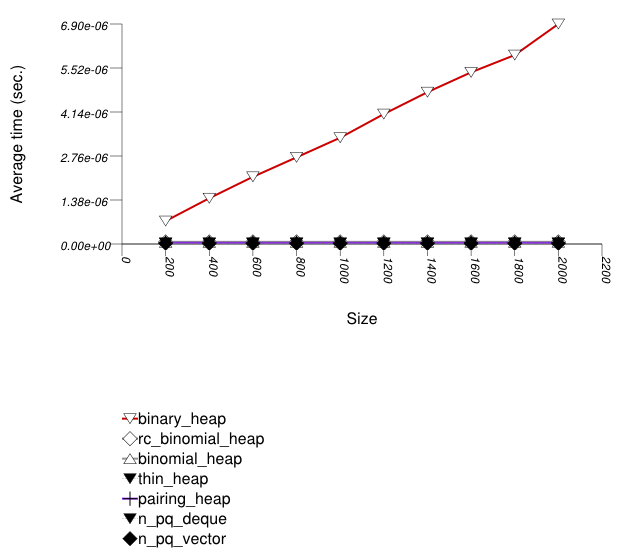
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The graphic below shows the results for the binary-heap based native priority queues and this library's priority_queue data structures.
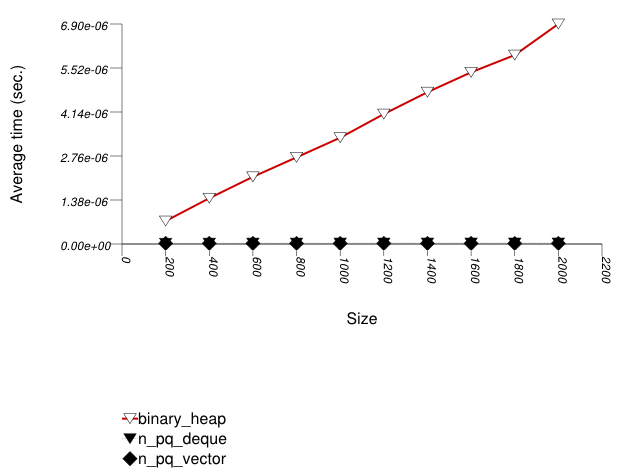
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue adapting std::vector
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
Binary heaps are the most suited for sequences of
push and pop operations of primitive types
(e.g. ints). They are less constrained
than any other type, and since it is very efficient to store
such types in arrays, they outperform even pairing heaps. (See
Priority
Queue Text push Timing Test for the case of
non-primitive types.)
This test inserts a number of values with integer keys
into a container using push , then removes them
using pop . It measures the average time for
push and pop as a function
of the number of values.
It uses the test file:
performance/ext/pb_ds/priority_queue_random_int_push_pop_timing.cc
The test checks the effect of different underlying data structures.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
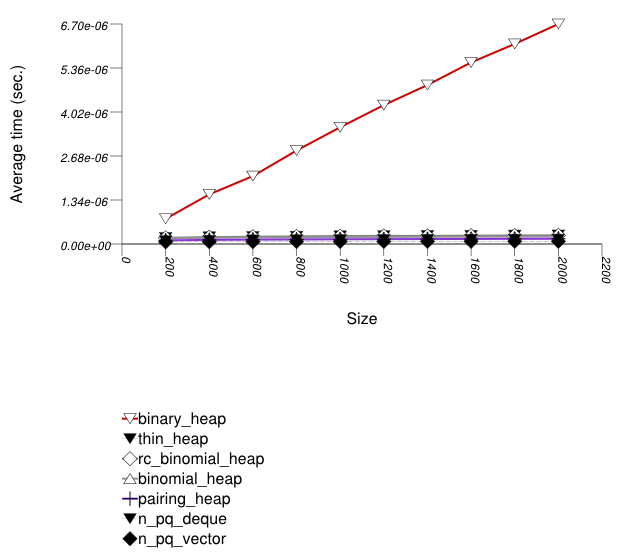
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
Binary heaps are the most suited for sequences of
push and pop operations of primitive types
(e.g. ints). This is explained in
Priority
Queue Random Int push Timing Test. (See Priority Queue
Text push Timing Test for the case of primitive
types.)
At first glance it seems that the standard's vector-based priority queue is approximately on par with this library's corresponding priority queue. There are two differences however:
The standard's priority queue does not downsize the underlying vector (or deque) as the priority queue becomes smaller (see Priority Queue Text
popMemory Use Test). It is therefore gaining some speed at the expense of space.From Priority Queue Random Integer
pushandpopTiming Test, it seems that the standard's priority queue is slower in terms ofpushoperations. Since the number ofpopoperations is at most that ofpushoperations, the test here is the "best" for the standard's priority queue.
This test inserts a number of values with keys from an arbitrary text ([ wickland96thirty ]) into a container, then pops them until only one is left in the container. It measures the memory use as a function of the number of values pushed to the container.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_pop_mem_usage.cc
The test checks the effect of different underlying data structures.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The priority queue implementations (excluding the standard's) use memory proportionally to the number of values they hold: node-based implementations (e.g., a pairing heap) do so naturally; this library's binary heap de-allocates memory when a certain lower threshold is exceeded.
Note from Priority Queue Text push
and pop Timing Test and Priority Queue
Random Integer push
and pop Timing Test that this does not
impede performance compared to the standard's priority
queues.
See Hash-Based Erase Memory Use Test for a similar phenomenon regarding priority queues.
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
two containers, then merges the containers. It uses
join for this library's priority queues; for
the standard's priority queues, it successively pops values from
one container and pushes them into the other. The test measures
the average time as a function of the number of values.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_join_timing.cc
The test checks the effect of different underlying data structures.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
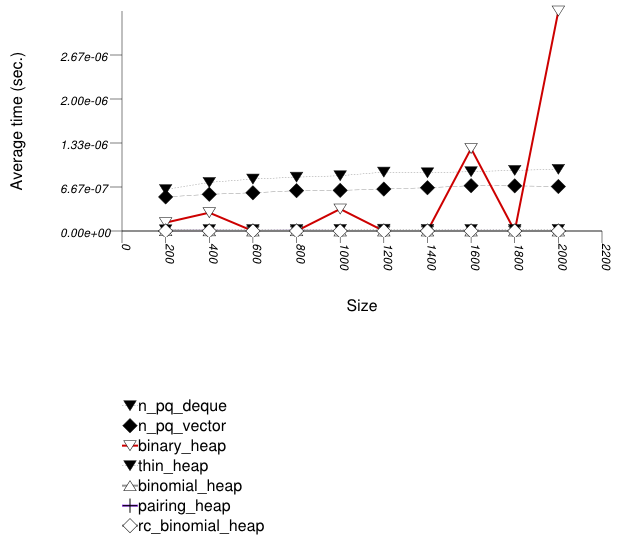
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
In this test the node-based heaps perform join in
either logarithmic or constant time. The binary heap requires
linear time, since the well-known heapify algorithm [clrs2001] is linear.
It would be possible to apply the heapify algorithm to the
standard containers, if they would support iteration (which they
don't). Barring iterators, it is still somehow possible to perform
linear-time merge on a std::vector-based
standard priority queue, using top()
and size() (since they are enough to expose
the underlying array), but this is impossible for
a std::deque-based standard priority queue.
Without heapify, the cost is super-linear.
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
into a container then modifies each one "up" (i.e., it
makes it larger). It uses modify for this library's
priority queues; for the standard's priority queues, it pops values
from a container until it reaches the value that should be
modified, then pushes values back in. It measures the average
time for modify as a function of the number of
values.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_modify_up_timing.cc
The test checks the effect of different underlying data structures for graph algorithms settings. Note that making an arbitrary value larger (in the sense of the priority queue's comparison functor) corresponds to decrease-key in standard graph algorithms [clrs2001].
The two graphics below show the results for the native priority_queues and this library's priority_queues.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
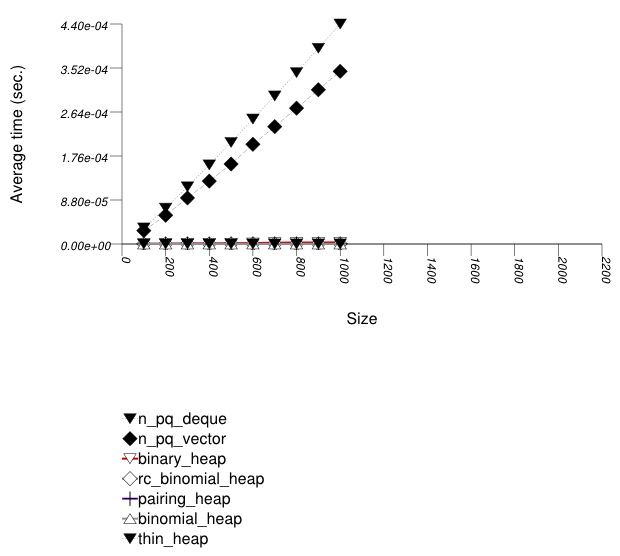
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The graphic below shows the results for the native priority queues and this library's pairing and thin heap priority_queue data structures.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
As noted above, increasing an arbitrary value (in the sense of
the priority queue's comparison functor) is very common in
graph-related algorithms. In this case, a thin heap
(priority_queue with
Tag = thin_heap_tag)
outperforms a pairing heap (priority_queue with
Tag = pairing_heap_tag).
Conversely, Priority Queue Text
push Timing Test, Priority Queue
Text push and pop Timing Test, Priority
Queue Random Integer push Timing Test, and
Priority
Queue Random Integer push and pop Timing
Test show that the situation is reversed for other
operations. It is not clear when to prefer one of these two
different types.
In this test this library's binary heaps
effectively perform modify in linear time. As explained in
Priority Queue Design::Traits, given a valid point-type iterator,
a binary heap can perform
modify logarithmically. The problem is that binary
heaps invalidate their find iterators with each modifying
operation, and so the only way to obtain a valid point-type
iterator is to iterate using a range-type iterator until
finding the appropriate value, then use the range-type iterator
for the modify operation.
The explanation for the standard's priority queues' performance
is similar to that in Priority Queue Text
join Timing Test.
This test inserts a number of values with keys from an
arbitrary text ([ wickland96thirty ]) into
into a container then modifies each one "down" (i.e., it
makes it smaller). It uses modify for this library's
priority queues; for the standard's priority queues, it pops values
from a container until it reaches the value that should be
modified, then pushes values back in. It measures the average
time for modify as a function of the number of
values.
It uses the test file:
performance/ext/pb_ds/priority_queue_text_modify_down_timing.cc
The main purpose of this test is to contrast Priority Queue
Text modify Up Timing Test.
The two graphics below show the results for the native priority_queues and this library's priority_queues.
The graphic immediately below shows the results for the native priority_queue type instantiated with different underlying container types versus several different versions of library's priority_queues.
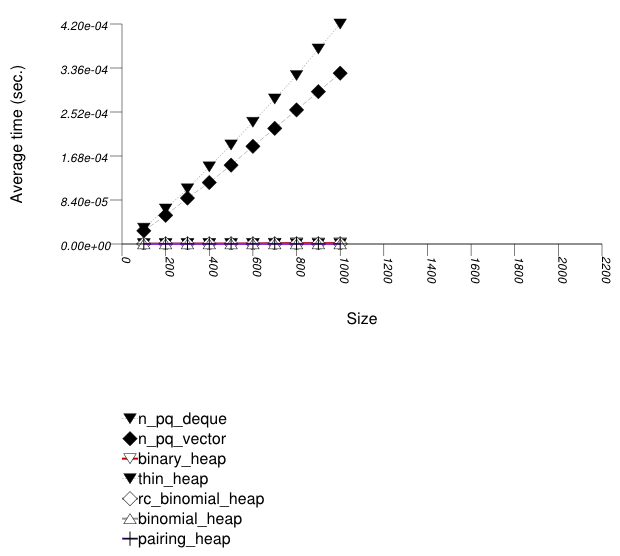
The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| n_pq_vector | ||
std::priority_queue
|
Sequence
|
std::vector
|
| n_pq_deque | ||
std::priority_queue
|
Sequence
|
std::deque
|
| binary_heap | ||
priority_queue
|
Tag
|
binary_heap_tag
|
| binomial_heap | ||
priority_queue
|
Tag
|
binomial_heap_tag
|
| rc_binomial_heap | ||
priority_queue
|
Tag
|
rc_binomial_heap_tag
|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
The graphic below shows the results for the native priority queues and this library's pairing and thin heap priority_queue data structures.

The abbreviated names in the legend of the graphic above are instantiated with the types in the following table.
| Name/Instantiating Type | Parameter | Details |
|---|---|---|
| thin_heap | ||
priority_queue
|
Tag
|
thin_heap_tag
|
| pairing_heap | ||
priority_queue
|
Tag
|
pairing_heap_tag
|
Most points in these results are similar to Priority Queue
Text modify Up Timing Test.
It is interesting to note, however, that as opposed to that
test, a thin heap (priority_queue with
Tag = thin_heap_tag) is
outperformed by a pairing heap (priority_queue with
Tag = pairing_heap_tag).
In this case, both heaps essentially perform an erase
operation followed by a push operation. As the other
tests show, a pairing heap is usually far more efficient than a
thin heap, so this is not surprising.
Most algorithms that involve priority queues increase values
(in the sense of the priority queue's comparison functor), and
so Priority Queue
Text modify Up Timing Test - is more interesting
than this test.
In general, hash-based containers have better timing performance than containers based on different underlying-data structures. The main reason to choose a tree-based or trie-based container is if a byproduct of the tree-like structure is required: either order-preservation, or the ability to utilize node invariants. If memory-use is the major factor, an ordered-vector tree gives optimal results (albeit with high modificiation costs), and a list-based container gives reasonable results.
Hash-based containers are typically either collision chaining or probing. Collision-chaining containers are more flexible internally, and so offer better timing performance. Probing containers, if used for simple value-types, manage memory more efficiently (they perform far fewer allocation-related calls). In general, therefore, a collision-chaining table should be used. A probing container, conversely, might be used efficiently for operations such as eliminating duplicates in a sequence, or counting the number of occurrences within a sequence. Probing containers might be more useful also in multithreaded applications where each thread manipulates a hash-based container: in the standard, allocators have class-wise semantics (see [meyers96more] - Item 10); a probing container might incur less contention in this case.
In hash-based containers, the range-hashing scheme seems to affect performance more than other considerations. In most settings, a mask-based scheme works well (or can be made to work well). If the key-distribution can be estimated a-priori, a simple hash function can produce nearly uniform hash-value distribution. In many other cases (e.g., text hashing, floating-point hashing), the hash function is powerful enough to generate hash values with good uniformity properties [knuth98sorting]; a modulo-based scheme, taking into account all bits of the hash value, appears to overlap the hash function in its effort.
The range-hashing scheme determines many of the other policies. A mask-based scheme works well with an exponential-size policy; for probing-based containers, it goes well with a linear-probe function.
An orthogonal consideration is the trigger policy. This presents difficult tradeoffs. E.g., different load factors in a load-check trigger policy yield a space/amortized-cost tradeoff.
In general, there are several families of tree-based underlying data structures: balanced node-based trees (e.g., red-black or AVL trees), high-probability balanced node-based trees (e.g., random treaps or skip-lists), competitive node-based trees (e.g., splay trees), vector-based "trees", and tries. (Additionally, there are disk-residing or network-residing trees, such as B-Trees and their numerous variants. An interface for this would have to deal with the execution model and ACID guarantees; this is out of the scope of this library.) Following are some observations on their application to different settings.
Of the balanced node-based trees, this library includes a red-black tree, as does standard (in practice). This type of tree is the "workhorse" of tree-based containers: it offers both reasonable modification and reasonable lookup time. Unfortunately, this data structure stores a huge amount of metadata. Each node must contain, besides a value, three pointers and a boolean. This type might be avoided if space is at a premium [austern00noset].
High-probability balanced node-based trees suffer the drawbacks of deterministic balanced trees. Although they are fascinating data structures, preliminary tests with them showed their performance was worse than red-black trees. The library does not contain any such trees, therefore.
Competitive node-based trees have two drawbacks. They are
usually somewhat unbalanced, and they perform a large number of
comparisons. Balanced trees perform one comparison per each
node they encounter on a search path; a splay tree performs two
comparisons. If the keys are complex objects, e.g.,
std::string, this can increase the running time.
Conversely, such trees do well when there is much locality of
reference. It is difficult to determine in which case to prefer
such trees over balanced trees. This library includes a splay
tree.
Ordered-vector trees use very little space [austern00noset]. They do not have any other advantages (at least in this implementation).
Large-fan-out PATRICIA tries have excellent lookup performance, but they do so through maintaining, for each node, a miniature "hash-table". Their space efficiency is low, and their modification performance is bad. These tries might be used for semi-static settings, where order preservation is important. Alternatively, red-black trees cross-referenced with hash tables can be used. [okasaki98mereable] discusses small-fan-out PATRICIA tries for integers, but the cited results seem to indicate that the amortized cost of maintaining such trees is higher than that of balanced trees. Moderate-fan-out trees might be useful for sequences where each element has a limited number of choices, e.g., DNA strings.
Different mapping semantics were discussed in the introduction and design sections.Here the focus will be on the case where a keys can be composed into primary keys and secondary keys. (In the case where some keys are completely identical, it is trivial that one should use an associative container mapping values to size types.) In this case there are (at least) five possibilities:
Use an associative container that allows equivalent-key values (such as
std::multimap)Use a unique-key value associative container that maps each primary key to some complex associative container of secondary keys, say a tree-based or hash-based container.
Use a unique-key value associative container that maps each primary key to some simple associative container of secondary keys, say a list-based container.
Use a unique-key value associative container that maps each primary key to some non-associative container (e.g.,
std::vector)Use a unique-key value associative container that takes into account both primary and secondary keys.
Stated simply: there is a simple answer for this. (Excluding option 1, which should be avoided in all cases).
If the expected ratio of secondary keys to primary keys is small, then 3 and 4 seem reasonable. Both types of secondary containers are relatively lightweight (in terms of memory use and construction time), and so creating an entire container object for each primary key is not too expensive. Option 4 might be preferable to option 3 if changing the secondary key of some primary key is frequent - one cannot modify an associative container's key, and the only possibility, therefore, is erasing the secondary key and inserting another one instead; a non-associative container, conversely, can support in-place modification. The actual cost of erasing a secondary key and inserting another one depends also on the allocator used for secondary associative-containers (The tests above used the standard allocator, but in practice one might choose to use, e.g., [boost_pool]). Option 2 is definitely an overkill in this case. Option 1 loses out either immediately (when there is one secondary key per primary key) or almost immediately after that. Option 5 has the same drawbacks as option 2, but it has the additional drawback that finding all values whose primary key is equivalent to some key, might be linear in the total number of values stored (for example, if using a hash-based container).
If the expected ratio of secondary keys to primary keys is large, then the answer is more complicated. It depends on the distribution of secondary keys to primary keys, the distribution of accesses according to primary keys, and the types of operations most frequent.
To be more precise, assume there are m primary keys, primary key i is mapped to ni secondary keys, and each primary key is mapped, on average, to n secondary keys (i.e., E(ni) = n).
Suppose one wants to find a specific pair of primary and
secondary keys. Using 1 with a tree based container
(std::multimap), the expected cost is
E(Θ(log(m) + ni)) = Θ(log(m) +
n); using 1 with a hash-based container
(std::tr1::unordered_multimap), the expected cost is
Θ(n). Using 2 with a primary hash-based container
and secondary hash-based containers, the expected cost is
O(1); using 2 with a primary tree-based container and
secondary tree-based containers, the expected cost is (using
the Jensen inequality [motwani95random])
E(O(log(m) + log(ni)) = O(log(m)) +
E(O(log(ni)) = O(log(m)) + O(log(n)),
assuming that primary keys are accessed equiprobably. 3 and 4
are similar to 1, but with lower constants. Using 5 with a
hash-based container, the expected cost is O(1); using 5
with a tree based container, the cost is
E(Θ(log(mn))) = Θ(log(m) +
log(n)).
Suppose one needs the values whose primary key matches some given key. Using 1 with a hash-based container, the expected cost is Θ(n), but the values will not be ordered by secondary keys (which may or may not be required); using 1 with a tree-based container, the expected cost is Θ(log(m) + n), but with high constants; again the values will not be ordered by secondary keys. 2, 3, and 4 are similar to 1, but typically with lower constants (and, additionally, if one uses a tree-based container for secondary keys, they will be ordered). Using 5 with a hash-based container, the cost is Θ(mn).
Suppose one wants to assign to a primary key all secondary keys assigned to a different primary key. Using 1 with a hash-based container, the expected cost is Θ(n), but with very high constants; using 1 with a tree-based container, the cost is Θ(nlog(mn)). Using 2, 3, and 4, the expected cost is Θ(n), but typically with far lower costs than 1. 5 is similar to 1.
The following table shows the complexities of the different
underlying data structures in terms of orders of growth. It is
interesting to note that this table implies something about the
constants of the operations as well (see Amortized push
and pop operations).
push | pop | modify | erase | join | |
|---|---|---|---|---|---|
std::priority_queue
| Θ(n) worst Θ(log(n)) amortized | Θ(log(n)) Worst | Θ(n log(n)) Worst [std note 1] | Θ(n log(n)) [std note 2] | Θ(n log(n)) [std note 1] |
priority_queue
<Tag =
pairing_heap_tag>
| O(1) | Θ(n) worst Θ(log(n)) amortized | Θ(n) worst Θ(log(n)) amortized | Θ(n) worst Θ(log(n)) amortized | O(1) |
priority_queue
<Tag =
binary_heap_tag>
| Θ(n) worst Θ(log(n)) amortized | Θ(n) worst Θ(log(n)) amortized | Θ(n) | Θ(n) | Θ(n) |
priority_queue
<Tag =
binomial_heap_tag>
| Θ(log(n)) worst O(1) amortized | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) |
priority_queue
<Tag =
rc_binomial_heap_tag>
| O(1) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) |
priority_queue<Tag =
thin_heap_tag>
| O(1) | Θ(n) worst Θ(log(n)) amortized | Θ(log(n)) worst O(1) amortized, or Θ(log(n)) amortized [thin_heap_note] | Θ(n) worst Θ(log(n)) amortized | Θ(n) |
[std note 1] This
is not a property of the algorithm, but rather due to the fact
that the standard's priority queue implementation does not support
iterators (and consequently the ability to access a specific
value inside it). If the priority queue is adapting an
std::vector, then it is still possible to reduce this
to Θ(n) by adapting over the standard's adapter and
using the fact that top returns a reference to the
first value; if, however, it is adapting an
std::deque, then this is impossible.
[std note 2] As
with [std note 1], this is not a
property of the algorithm, but rather the standard's implementation.
Again, if the priority queue is adapting an
std::vector then it is possible to reduce this to
Θ(n), but with a very high constant (one must call
std::make_heap which is an expensive linear
operation); if the priority queue is adapting an
std::deque, then this is impossible.
[thin_heap_note] A thin heap has
Θ(log(n)) worst case modify time
always, but the amortized time depends on the nature of the
operation: I) if the operation increases the key (in the sense
of the priority queue's comparison functor), then the amortized
time is O(1), but if II) it decreases it, then the
amortized time is the same as the worst case time. Note that
for most algorithms, I) is important and II) is not.
In many cases, a priority queue is needed primarily for
sequences of push and pop operations. All of
the underlying data structures have the same amortized
logarithmic complexity, but they differ in terms of
constants.
The table above shows that the different data structures are
"constrained" in some respects. In general, if a data structure
has lower worst-case complexity than another, then it will
perform slower in the amortized sense. Thus, for example a
redundant-counter binomial heap (priority_queue with
Tag = rc_binomial_heap_tag)
has lower worst-case push performance than a binomial
heap (priority_queue
with Tag = binomial_heap_tag),
and so its amortized push performance is slower in
terms of constants.
As the table shows, the "least constrained" underlying data structures are binary heaps and pairing heaps. Consequently, it is not surprising that they perform best in terms of amortized constants.
Pairing heaps seem to perform best for non-primitive types (e.g.,
std::strings), as shown by Priority Queue TextpushTiming Test and Priority Queue TextpushandpopTiming Testbinary heaps seem to perform best for primitive types (e.g., ints), as shown by Priority Queue Random Integer
pushTiming Test and Priority Queue Random IntegerpushandpopTiming Test.
In some graph algorithms, a decrease-key operation is
required [clrs2001];
this operation is identical to modify if a value is
increased (in the sense of the priority queue's comparison
functor). The table above and Priority Queue
Text modify Up Timing Test show that a thin heap
(priority_queue with
Tag = thin_heap_tag)
outperforms a pairing heap (priority_queue with
Tag = Tag = pairing_heap_tag),
but the rest of the tests show otherwise.
This makes it difficult to decide which implementation to use in
this case. Dijkstra's shortest-path algorithm, for example, requires
Θ(n) push and pop operations
(in the number of vertices), but O(n2)
modify operations, which can be in practice Θ(n)
as well. It is difficult to find an a-priori characterization of
graphs in which the actual number of modify
operations will dwarf the number of push and
pop operations.